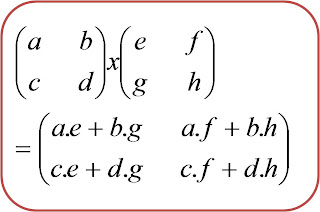Senin, 28 Januari 2013
Exist - mencari alasan
Iklasnya hati sering kali disalah arti
Manis di bibir memutar kata
Engkau pasti tersenyum dengan pengunduran diriku
Ada baiknya bila tidak lagi bersama
Rumus Matematika untuk Ujian Nasional SMK (Akuntansi)
Menyelesaikan masalah berkaitan dengan persentase untung atau rugi dari suatu kegiatan ekonomi
1. Mencari harga jual jika persentase untung/rugi dan harga beli diketahui:
=> Jika untung harga jual = 100+% untung x harga beli
100
=> Jika rugi harga jual = 100-% rugi x harga beli
100
2. Mencari harga beli jika persentase untung/rugi dan harga jual diketahui:
=> Jika untung harga beli = 1 0 0 x harga jual
100+% untung
=> Jika rugi harga beli = 1 0 0 x harga jual
100-% rugi
Menyelesaikan masalah yang berkaitan dengan perbandingan
Jarak sebenarnya = Jarak pada peta x Skala
Contoh :
1. Diketahui jarak pada peta 2 cm. Berapa jarak sebenarnya bila skala tersebut 1 : 500
Jawab :
Jarak sebenarnya : jarak pada peta x skala
Jarak sebenarnya : 2 cm x 500 = 1000 cm
2. Berapakah Perbandingan dari 35 : 25 : 5
Jawab : 35 : 25 : 5 Di bagi angka yg terkecil
7 : 5 : 1
3. Berapakah hasil perbandingan 4 : 2 : 1 dari 98 buah kelereng
Jawab : x 98 = 4 x 14 = 56 (14 dari 1+2+4)
x 98 = 2 x 14 = 28
x 98 = 1 x 14 = 14
4. Berapa hasil perbandingan 3 : 6 dari 81
Jawab : x 81 = 3 x 9 = 27 (9 dari 3+6)
x 81 = 6 x 9 = 63
5. Berapa umur budi dan ani jika perbandingan 3 : 7 dan selisih umur mereka 12
Jawab : x 12 = 3 x 3 = 9
x 12 = 7 x 3 = 21
Menentukan penyelesaian sistem persamaan linier dua variabel
, 
Menyelesaikan pertidaksamaan kuadrat
1. Memfaktorkan 
diuraikan menjadi 
2. Rumus
ABC: 
3. a. 
b. 
c. 
d. 
e. 
4. Menyusun persamaan kuadrat
Menghitung hasil operasi matriks.
a. Penjumlahan atau pengurangan matriks
Matriks A dan B dapat dijumlahkan atau dikurangkan jika ordo A = ordo B
b. Perkalian Matriks dengan Skalar
c. Perkalian Dua Matriks
d. Transpos Matriks
e. Invers matriks
Bila 
maka invers dari A adalah :
Syarat ad-bc 
0
Menentukan ingkaran dari suatu pernyataan
Negasi dari n = 3 adalah n tidak = 3.
Negasi dari dia benar adalah dia tidak benar.
Negasi dari saya lapar adalah saya tidak lapar.
Bagaimana dengan negasi suatu implikasi?
JIKA Rano bekerja MAKA Rano mendapat gaji.
Bagaimana menurut Anda?
Orang pada umumnya mengira negasi dari pernyataan implikasi di atas adalah:
JIKA Rano tidak bekerja MAKA Rano tidak mendapat gaji.
Bukan. Pernyataan di atas bukanlah negasinya. Beberapa alternatif yang lain adalah:
JIKA Rano bekerja MAKA Rano tidak mendapat gaji.
JIKA Rano tidak mendapat gaji MAKA Rano tidak bekerja.
Pernyataan di atas masih bukan negasinya.
Negasi yang tepat adalah:
Rano bekerja DAN Rano tidak mendapat gaji.
Atau:
Rano bekerja TAPI Rano tidak mendapat gaji.
(DAN = TAPI).
JIKA segitiga sama sisi MAKA besar jumlah ketiga sudutnya adalah 180 derajat.
Negasinya:
Segitiga sama sisi TETAPI besar jumlah ketiga sudutnya adalah tidak 180 derajat.
Jadi,
negasi dari p ==> q adalah p DAN ~q
Menentukan kesimpulan yang sah berdasarkan aturan penarikan kesimpulan dari dua buah premis yang diketahui
Cara menarik kesimpulan kita kali ini berdasarkan prinsip logika implikasi saja.
Jika SYARAT terpenuhi maka HASIL terpenuhi.
Cara 1: POsitif syarat, modus ponens
Premis: SYARAT terpenuhi
Kesimpulan:HASIL terpenuhi
Contoh:
Premis 1:Jika BERIMAN maka BERPUASA
Premis 2: BERIMAN
Kesimpulan: BERPUASA
Cara 2: TOlak hasil, modus tollens
Premis: HASIL TIDAK terpenuhi
Kesimpulan: (karena) SYARAT TIDAK terpenuhi
Contoh:
Premis 1: Jika BERIMAN maka BERPUASA
Premis 2: TIDAK BERPUASA
Kesimpulan: TIDAK BERIMAN
Cara 3: silogisme, runtuntan logis.
Contoh:
Jika BERIMAN maka BERPUASA
Jika BERPUASA maka BERTAKWA
Kesimpulan: Jika BERIMAN maka BERTAKWA.
Menentukan salah satu unsur pada perhitungan keseimbangan pasar, jika diketahui fungsi permintaan dan fungsi penawaran
Rumus Keseimbangan Pasar :
Qd = Qs
Keterangan :
Qd : jumlah permintaan
Qs : jumlah penawaran
Menentukan persamaan fungsi kuadrat, jika diberikan grafiknya dan atau sebaliknya
a. y = – 2x² + 4x + 3
b. y = – 2x² + 4x + 2
c. y = – x² + 2x + 3
d. y = – 2x² + 4x – 6
e. y = – x² + 2x – 5
Soal di atas dapat diselesaikan dengan logika sederhana hubungan koordinat titik .
secara umum fungsi kuadrat berbentuk y = f(x) = ax² + bx + c. Dari soal diketahui fungsi kuadrat di atas melalui titik ( 1,4 ) dan titik ( 0,3 ). Jika nilai x = 0 kita subtitusikan pada persamaan kuadrat akan didapat :
y = f(0) = a(0²) + b.0 + c maka akan didapat koordinat ( 0,c ), kalau diperhatikan option jawaban maka akan kita dapat bahwa jawaban yang mungkin adalah option A atau option C
Langkah berikutnya kita cek titik ( 1,4 ) pada persamaan fungsi kuadrat
pada option A. y = – 2x² + 4x + 3, jika kita subtitusi nilai x = 1 ternyata akan didapat hasil :
f(1) = –2(1²) + 4.1 + 3 = –2 + 4 + 3 = 5 ( ini tidak cocok, sebab titik yang diharapkan (1,4)
pada option C. y = – x² + 2x + 3, jika kita subtitusi nilai x = 1 ternyata akan didapat hasil :
f(1) = –(1²) + 2.1 + 3 = –1 + 2 + 3 = 4 ( ini cocok dengan titik yang diharapkan (1,4) )
so, the answer is C
Menentukan rumus umum atau salah satu unsur dari suatu barisan aritmetika atau geometri
* Deret Geometri
* Barisan Geometri
Menghitung keliling dan luas bangun datar
A. Persegi Luas = sisi x sisi x 1 ukuran persegi
Keliling = 4 x sisi x 1 ukuran panjang
sisi = Akarkan Luas
sisi = Keliling dibagikan 4
_______________________________________________________________
B. Persegi Panjang
Luas = Panjang x Lebar x 1 Ukuran Persegi
Keliling = 2 x (Panjang + Lebar) x 1 Ukuran Panjang
_______________________________________________________________
C. Segitiga
Luas = ½ x Alas x Tinggi x 1 Ukuran Persegi
Keliling = s + s + s x 1 Ukuran Panjang
_______________________________________________________________
D. Lingkaran
Luas = 22/7 atau 3,14 x Jari-jari (r) x r x 1 Ukuran Persegi
Keliling = 22/7 atau 3,14 x Diameter (d) x 1 Ukuran Panjang
r = d dibagi 2
d = r dikali 2
_______________________________________________________________
E. Trapesium
Luas = ½ x (Jumlah Sisi Sejajar) x Tinggi x 1 Ukuran Persegi
Keliling = Sisi + Sisi + Sisi + Sisi x 1 Ukuran Panjang
_______________________________________________________________
F. Jajaran Genjang
Luas = Alas x Tinggi x 1 Ukuran Persegi
Keliling = Sisi + Sisi + Sisi + Sisi x 1 Ukuran Panjang
_______________________________________________________________
G. Layang – layang
Luas = ½ x Diagonal 1 x Diagonal 2 x 1 Ukuran Persegi
Keliling = Sisi + Sisi + Sisi + Sisi x 1 Ukuran Panjang
_______________________________________________________________
H. Belah Ketupat
Luas = ½ x Diagonal x Diagonal x 1 Ukuran Persegi
Keliling = Sisi + Sisi + Sisi + Sisi x 1 Ukuran
Menyelesaikan permasalahan yang berkaitan dengan permutasi atau kombinasi dan peluang
A. Permutasi 
§
Permutasi dengan
beberapa unsur yang sama 
n = banyak unsur
a dan b = banyaknya unsur-unsur yang sama.
Contoh: Berapa banyak susunan huruf yang berbeda pada satu baris yang dibentuk dari huruf-huruf pada kata “KALKULUS”
Jawab: Terdiri atas 8 huruf,maka n = 8. Huruf yang sama yaitu: K = 2, L = 2, dan U = 2
Maka banyaknya permutasi=
§
Permutasi Siklis 
n = banyaknya unsur
Contoh: Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan urutan yang berbeda?
Jawab: 
B. Kombinasi 
Contoh: Dari 8 pelajar akan dipilih 5 pelajar untuk mengikuti pelajar teladan. Berapa banyak cara memilih pelajar tersebut?
Jawab: banyaknya kombinasi 5 dari 8 siswa =
C. Peluang
Suatu Kejadian 
Peluang A = 
· Peluang kejadian yang saling berkomplemen 
Contoh: Peluang Andi masuk di PTN adalah 0,3. Berapa peluang Andi gagal masuk PTN.
Jawab: A= kejadian Andi masuk di PTN = P(A)=0,3
A’= kejadian Andi gagal masuk PTN = P(B)
Jadi P(A) = 1-P(A) = 1-0,3=0,7
· Peluang Dua Kejadian yang saling Lepas (Saling Asing) Secara Umum Untuk Setiap Kejadian A dan B
Untuk kejadian
A dan B yang saling lepas maka 
Jadi jika A dan B saling lepas maka 
· Peluang Dua Kejadian yang Saling Bebas (jika kejadian A dan B tuidak saling mempengaruhi)
Menentukan ukuran pemusatan dan penyebaran data
1. Rata-Rata (Mean)
= rata-rata, dibaca “x bar”
n = banyaknya data
= nilai data ke-I (I = 1,2,3,…,n)
Rata-Rata Gabungan 
2. Median (Me) = nilai tengah
· Median 
· Median 
· Median 
3. Modus (Mo) = datum yang sering muncul 
L = tepi bawah kelas
= selisih frekuensi kelas modus dengan kelas
sebelumnya
= selisih frekuensi kelas modus dengan kelas
sesudahnya
p = interval (lebar/panjang kelas)
4. Kuartil (Q)
· Data Tunggal letak 
= kuartil ke-i; n = banyaknya data; i = 1,2,3
L = tepi bawah kelas
fk = frekuensi kumulatif sebelum kuartil ke-i
f = frekuensi kelas kuartil ke-i
p = interval (lebar/panjang kelas)
B. Ukuran Penyebaran Data
1. Jangkauan (range) = selisih antara datum terbesar dengan datum terkecil
2. Jangkauan
Antar Kuartil 
3. Jangkauan
Semi Kuartil (Simpangan Kuartil) 
4. Simpangan
Rata-Rata 
atau 
= datum ke-I; = rata-rata; n = banyak datum; 
= frekuensi kelas ke-i
5.
Ragam (Variasi) 
atau 
6.
Simpangan Baku
(Standar Deviasi) 
atau
Menyelesaikan permasalahan yang berkaitan dengan bunga tunggal, majemuk, rente, anuitas, penyusutan
Langganan:
Postingan (Atom)